AHORA HABLAREMOS 

SOBRE TEOREMAS ..

Teorema de Bayes

El teorema de Bayes es utilizado para calcular la probabilidad de un suceso, teniendo información de antemano sobre ese suceso.

Podemos calcular la probabilidad de un suceso A, sabiendo además que ese A cumple cierta característica que condiciona su probabilidad. El teorema de Bayes entiende la probabilidad de forma inversa al teorema de la probabilidad total. El teorema de la probabilidad total hace inferencia sobre un suceso B, a partir de los resultados de los sucesos A. Por su parte, Bayes calcula la probabilidad de A condicionado a B.

El teorema de Bayes ha sido muy cuestionado. Lo cual se ha debido, principalmente, a su mala aplicación. Ya que, mientras se cumplan los supuestos de sucesos disjuntos y exhaustivos, el teorema es totalmente válido.

Fórmula del teorema de Bayes

Para calcular la probabilidad tal como la definió Bayes en este tipo de sucesos, necesitamos una fórmula. La fórmula se define matemáticamente como:

Donde B es el suceso sobre el que tenemos información previa y A(n) son los distintos sucesos condicionados. En la parte del numerador tenemos la probabilidad condicionada, y en la parte de abajo la probabilidad total. En cualquier caso, aunque la fórmula parezca un poco abstracta, es muy sencilla. Para demostrarlo, utilizaremos un ejemplo en el que en lugar de A(1), A(2) y A(3), utilizaremos directamente A, B y C.

Ejemplo del teorema de Bayes

Una empresa tiene una fábrica en Estados Unidos que dispone de tres máquinas A, B y C, que producen envases para botellas de agua. Se sabe que la máquina A produce un 40% de la cantidad total, la máquina B un 30%, y la máquina C un 30%. También se sabe que cada máquina produce envases defectuosos. De tal manera que la máquina A produce un 2% de envases defectuosos sobre el total de su producción, la máquina B un 3%, y la máquina C un 5%. Dicho esto, se plantean dos cuestiones:

P(A) = 0,40 P(D/A) = 0,02

P(B) = 0,30 P(D/B) = 0,03

P(C) = 0,30 P(D/C) = 0,05

1. Si un envase ha sido fabricado por la fábrica de esta empresa en Estados Unidos ¿Cuál es la probabilidad de que sea defectuoso?

Se calcula la probabilidad total. Ya que, a partir los diferentes sucesos, calculamos la probabilidad de que sea defectuoso.

P(D) =[ P(A) x P(D/A) ] + [ P(B) x P(D/B) ] + [ P(C) x P(D/C) ] = [ 0,4 x 0,02 ] + [ 0,3 x 0,03 ] + [ 0,3 x 0,05 ] = 0,032

Expresado en porcentaje, diríamos que la probabilidad de que un envase fabricado por la fábrica de esta empresa en Estados Unidos sea defectuoso es del 3,2%.

Siguiendo con la pregunta anterior, si se adquiere un envase y este es defectuoso ¿Cuáles es la probabilidad de que haya sido fabricado por la máquina A? ¿Y por la máquina B? ¿Y por la máquina C?

Aquí se utiliza el teorema de Bayes. Tenemos información previa, es decir, sabemos que el envase es defectuoso. Claro que, sabiendo que es defectuoso, queremos saber cuál es la probabilidad de que se haya producido por una de las máquinas.

P(A/D) = [P(A) x P(D/A)] / P(D) = [0,40 x 0,02] / 0,032 = 0,25

P(B/D) = [P(B) x P(D/B)] / P(D) = [0,30 x 0,03] / 0,032 = 0,28

P(C/D) = [P(C) x P(D/C)] / P(D) = [0,30 x 0,05] / 0,032 = 0,47

Sabiendo que un envase es defectuoso, la probabilidad de que haya sido producido por la máquina A es del 25%, de que haya sido producido por la máquina B es del 28% y de que haya sido producido por la máquina C es del 47%.

Teorema de la probabilidad total

El teorema de la probabilidad total, establece que:

Sean A1, A2, A3, … , An, eventos que forman una partición del espacio muestral S, y sea B otro evento cualquiera del espacio muestral S, entonces la probabilidad del evento B se puede obtener de la siguiente manera:

Los problemas de probabilidades que requieren al teorema de probabilidad total, también se pueden resolver de manera sencilla usando el diagrama de árbol. Vamos a revisar 1 ejercicio, y lo vamos a resolver con el diagrama de árbol y con el teorema.

---

Ejercicio 1:

En un acuario se tienen solo 2 especies de peces, el 40% son de la especie azul y el 60% son de la especie roja. De la especie azul, el 30% son machos; mientras que, de la especie roja, el 40% son hembras. ¿Cuál es la probabilidad de que un pez elegido aleatoriamente en el acuario sea macho?

Solución con el diagrama de árbol:

A partir de los datos del enunciado, vamos a elaborar el diagrama de árbol.

Recuerda el truco que usamos para calcular probabilidades usando el diagrama de árbol: cuando avanzamos de izquierda a derecha, multiplicamos las probabilidades; cuando avanzamos de arriba hacia abajo, sumamos las probabilidades.

La probabilidad de encontrar un macho, seleccionando un pez de forma aleatoria es de 0,48 o 48%.

Solución con el teorema de probabilidad total:

Ahora resolvemos el mismo problema usando el teorema. Tenemos 2 eventos A1 y A2, que forman una partición del espacio muestral S (peces del acuario):

• A1: que un pez elegido aleatoriamente sea de la especie azul.
• A2: que un pez elegido aleatoriamente sea de la especie roja.

A partir del gráfico, sabemos que:

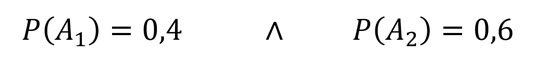
También tenemos al evento B:

• B: que un pez elegido aleatoriamente sea macho.

Nos dicen que de la especie azul, el 30% son machos. Por ello, sabemos que la probabilidad de que un pez sea macho, dado que es de la especie azul, es de:

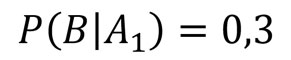
Nos dicen que el 40% de los peces de la especia roja son hembras, por ello, el 60% serán machos. Entonces, sabemos que la probabilidad de que un pez sea macho, dado que es de la especie roja:

Recordemos el teorema de probabilidad total:

En nuestro caso, tenemos una partición del espacio muestral S, formada solo por 2 eventos: A1 y A2 .

Reemplazando nuestros valores:

La probabilidad de que un pez elegido aleatoriamente sea macho, es de 0,48 o 48 %.

PROBABILIDAD CONDICIONAL

     La probabilidad condicional es aquella que nos indica probabilidad de que un evento X ocurra si ha ocurrido un evento Y. Por ejemplo: si tengo 5 cachorros, de los cuales 3 son blancos y 2 son negros. De los 3 blancos, 1 tiene manchas y de los 2 negros, 1 tiene manchas. ¿Cuál es la probabilidad de elegir al azar uno blanco y que sea rayado?

El teorema de Bayes se aplica para obtener las probabilidades condicionadas de ciertos eventos dada la probabilidad de ocurrencias condicionadas de otros eventos. Por ejemplo: la probabilidad de tener un dolor de cabeza dado que se tiene gripe, se podría saber (si se tiene algún dato más), la probabilidad de tener gripe si se tiene un dolor de cabeza.

La probabilidad condicional relaciona eventos que no son mutuamente excluyentes. Es decir, uno depende de otro para suceder. Mientras que el Teorema de Bayes relaciona una probabilidad condicional teniendo presente los efectos observados.